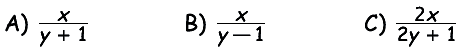I quesiti dal N. 1 al N. 10 valgono 3 punti ciascuno
Per ogni quesito, tra le 5 risposte proposte, una sola è giusta.

1. Qual è il più piccolo numero di interi consecutivi la cui somma vale 201120112011?
A) B) C) D) E)
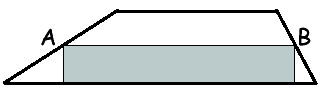
2. In figura vedi un trapezio. A e B sono i punti medi dei lati obliqui e l’area del rettangolo ombreggiato vale 13 cm2. Quanti cm2 misura l’area del trapezio?
A) B) C) D) E)
3. Se sommo le lunghezze di tre dei lati di un rettangolo assegnato, posso ottenere come risultato 20 o 22. Quanto vale il perimetro del rettangolo?

A) B) C) D) E)
4. Poniamo X = 122 x 123 + 123 x 124 + 124 x 125, Y = 1222 + 1232 + 1242, Z = 121 x 122 + 122 x 123 + 123 x 124. Quale delle seguenti relazioni è vera?
A) B) C) D) E)
5. In un teatro vi sono 100 spettatori: 50 di essi sono italiani, 60 sono maschi, 90 sono vegetariani. Di quanti spettatori presenti in quel teatro si può essere certi che siano allo stesso tempo italiani, maschi e vegetariani?

A) B) C) D) E)
6. Un mosaico rettangolare di area 360 cm2è ottenuto accostando piastrelle quadrate, tutte della stessa taglia. Un lato del mosaico misura 24 cm, l’altro misura 5 volte il lato delle piastrelle. Quanto vale, in cm2, l’area di ogni piastrella?
A) B) C) D) E)
7. Supponiamo di scrivere in ordine decrescente tutti i numeri interi positivi
di 4 cifre significative (cioè tali che la cifra delle migliaia non sia 0), la somma delle cui cifre è 4. Che posizione occupa in questa lista il numero 2011?
A) B) C) D) E)
8. Osserva la figura 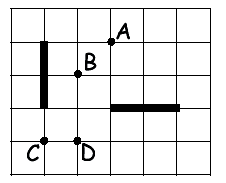: ognuno dei due segmenti evidenziati è ottenibile dall’altro per rotazione. Quali dei punti evidenziati sono centri di tali rotazioni?
A) B) C) D) E)

9. LLa regione in figura è scomponibile, come indicato, in un esagono regolare di lato 1, sei triangoli e sei quadrati.
Quanto misura il suo perimetro?
Quanto misura il suo perimetro?
A) B) C) D) E)
10. Tre dadi regolari (cioè tali che la somma dei punti su facce opposte sia sempre 7) sono impilati come indica la figura 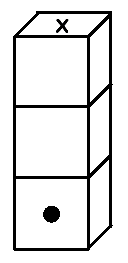. Del dado più basso è indicata la faccia con 1 punto. Inoltre sai che, ogni volta che due facce di dadi diversi combaciano, la somma dei punti sulle due facce è 5. Quanti punti ci sono sulla faccia contrassegnata con X?
A) B) C) D) E)

I quesiti dal N. 11 al N. 20 valgono 4 punti ciascuno

11. In un certo mese di un certo anno ci sono 5 lunedì, 5 martedì e 5 mercoledì. Nel mese precedente ci sono solo 4 domeniche. Allora

A) B) C) D) E)

12. Tre piloti, Michael, Fernando e Sebastian, prendono parte ad una gara di Formula 1. Appena partiti è in testa Michael, Fernando è secondo e Sebastian terzo. Durante la gara Michael e Fernando si scambiano di posizione 9 volte, Fernando e Sebastian 10 volte e Michael e Sebastian 11 volte. In che ordine finiscono la gara?

A) B) C) D) E)

13. Se 9n+ 9n+ 9n= 32011, quanto vale n?

A) B) C) D) E)

14. Nella griglia 3x3 in figura sono visibili 5 numeri. Nicola ne ha inserito uno in ogni cella che appare libera in modo che la somma dei numeri presenti in ogni sotto-griglia 2x2 valga 10 (le sottogriglie possono essere realizzate solo troncando righe e colonne consecutive). Quanto vale la somma dei numeri inseriti da Nicola?
A) B) C) D) E)
15. Ada afferma che Bice sta mentendo. Bice afferma che Carla sta mentendo. Carla afferma che Bice sta mentendo. Daniela afferma che Ada sta mentendo. Quante fra queste quattro ragazze stanno mentendo?

A) B) C) D) E)
16. In figura 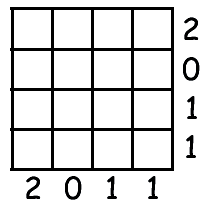vedi una griglia 4x4. Devi annerire alcune celle della griglia in modo che, per ogni riga, il numero di celle della riga annerite coincida con il numero indicato a destra della riga stessa e, per ogni colonna, il numero di
celle della colonna annerite coincida con il numero indicato ai piedi della colonna stessa. In quanti diversi modi puoi farlo?
A) B) C) D) E)
17. Qual è il maggior numero di numeri interi consecutivi di tre cifre che hanno almeno una cifra dispari?

A) B) C) D) E)
18. Ho due recipienti a forma di cubo; il lato del più grande è lungo un decimetro in più del lato dell’altro. Il più grande è pieno d’acqua, l’altro è vuoto. Se io travaso l’acqua dal recipiente grande al piccolo fino a riempirlo, nel recipiente grande rimangono 217 litri d’acqua. Quale è, in litri, la capacità del recipiente piccolo?
A) B) C) D) E)
19. Durante un viaggio in auto su una strada accidentata, Michela ha tracciato lo schizzo che vedi in figura 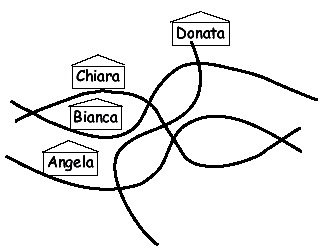: esso indica le case delle sue quattro amiche, le vie in cui abitano e gli incroci fra queste vie. Nella realtà però via Freccia, via Righello e via Chiodo sono tutte vie rettilinee. La quarta via è via Curva. Quale delle quattro amiche abita in via Curva?
A) B) C) D) E)
20. I numeri x e y sono entrambi maggiori di 1. Tra le seguenti frazioni, quale ha il valore più alto?

A) B) C) D) E)

I quesiti dal N. 21 al N. 30 valgono 5 punti ciascuno

21. Simone ha un cubo di vetro di un decimetro di lato. Usando degli adesivi dorati a forma di quadrato, tutti uguali fra loro, ha decorato la superficie del cubo come indicato dalla figura , in modo che le facce del cubo presentino tutte la stessa decorazione.
Qual è, in centimetri quadrati, l’area della porzione della superficie del cubo che appare dorata?

A) B) C) D) E)
22. Diciamo che un numero intero positivo di 5 cifre significative tutte diverse fra loro è “interessante” se la sua prima cifra è la somma delle rimanenti quattro. Quanti numeri interessanti esistono?

A) B) C) D) E)
23. In un triangolo ABC, sul lato BC viene scelto un punto D e sul segmento AD viene scelto un punto E. Si vengono così a determinare 9 angoli denotati con le cifre da 1 a 9, come indicato nella figura 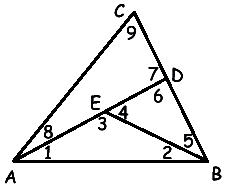. Qualunque sia il triangolo ABC, alcuni di questi angoli risultano necessariamente a due a due diversi fra loro. Nelle configurazioni in cui ve ne sono il meno possibile, quanti sono?
A) B) C) D) E)
24. Marco scrive gli interi da 1 a 9 in un ordine casuale. Per ogni coppia di interi che, in quell’ordine, risultano adiacenti, Marco calcola quindi la media aritmetica dei due interi. Infine, somma tutte le medie aritmetiche calcolate. Qual è il più grande valore che può ottenere?
A) B) C) D) E)
25. La figura 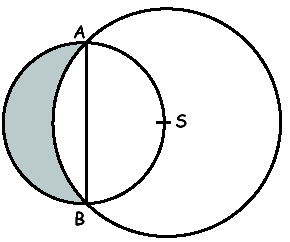mostra due circonferenze di raggi diversi. I punti A e B stanno su entrambe. Il segmento AB è un diametro di quella di raggio minore, la quale passa per il centro S di quella di raggio maggiore. Quest’ultima ha raggio 1. Quanto vale l’area della regione ombreggiata?
A) B) C) D) E)
26. Quante quaterne di spigoli di un cubo sono tali che, comunque si scelgano due spigoli nella quaterna, questi non abbiano vertici in comune? (Se due quaterne non coincidono, ma sono ottenibili l’una dall’altra per rotazione del cubo, vanno considerate diverse.)
A) B) C) D) E)
27. Per ogni intero n > 2, denotiamo con «n» il più grande numero primo che non supera n. Da quanti interi positivi k è soddisfatta l’equazione

A) B) C) D) E)
28. Hai una griglia 5x5 e vuoi annerirne alcune celle in modo che in ogni sottogriglia 3x3 vi siano esattamente n celle annerite. Per quali interi n, da 1 a 8 inclusi, puoi raggiungere lo scopo? (Le sotto-griglie possono essere realizzate troncando solo righe e colonne consecutive.)
A) B) C) D) E)
29. Assegnato un tetraedro regolare ABCD, sia il piano contenente la faccia ABC e s la retta in contenente lo spigolo BC. Sia quindi BCDE il tetraedro regolare che ha in comune con ABCD solo la faccia BCD. Dove la retta passante per D e E interseca il piano ?
A) B) C) D) E)
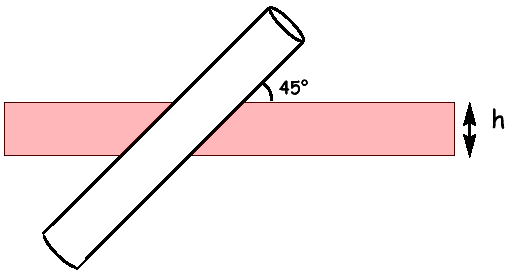
30. Un cilindro circolare retto con la base di raggio 2, verniciato di bianco, viene posto su una striscia rettangolare di stoffa rossa di ampiezza h, inclinato di 45 gradi rispetto alla striscia come mostra la figura.

La striscia viene avvolta, mantenendola in tensione, attorno al cilindro. Osservando ora il cilindro, si nota una spirale rossa data dalla striscia e una spirale bianca data dalla parte di cilindro non coperta dalla striscia. Quanto deve valere l’ampiezza h della striscia rossa se vogliamo che le due spirali abbiano la stessa ampiezza?
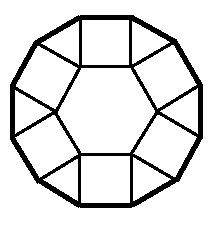A) B) C) D) E)
________